เซต (Set)
เมื่อพูดถึงเซตในเชิงคณิตศาสตร์ จะหมายถึงกลุ่มของอะไรบางอย่าง เรานิยมเขียนชื่อเซตด้วยอักษรตัวพิมพ์ใหญ่ เช่น
ให้ A เป็นเซตของผลไม้, A = {สับปะรด, ทุเรียน, มังคุด, ลำไย, ลิ้นจี่} จำนวนสมาชิกของ A, n(A)=5
ให้ B เป็นเซตสีของรุ้ง จะได้ B = {สีม่วง, สีคราม, สีน้ำเงิน, สีเขียว, สีเหลือง, สีแสด, สีแดง} และ n(B)=7
เมื่อพูดถึงเซตในเชิงคณิตศาสตร์ จะหมายถึงกลุ่มของอะไรบางอย่าง เรานิยมเขียนชื่อเซตด้วยอักษรตัวพิมพ์ใหญ่ เช่น
ให้ A เป็นเซตของผลไม้, A = {สับปะรด, ทุเรียน, มังคุด, ลำไย, ลิ้นจี่} จำนวนสมาชิกของ A, n(A)=5 ให้ B เป็นเซตสีของรุ้ง จะได้ B = {สีม่วง, สีคราม, สีน้ำเงิน, สีเขียว, สีเหลือง, สีแสด, สีแดง} และ n(B)=7
ถ้าเราสามารถเขียนและนับจำนวนสมาชิกในเซตได้ชัดเจนแบบนี้ จะเรียกว่าเป็นเซตจำกัด (Finite Set) จะใช้สัญลักษณ์ 
แทนคำว่า “เป็นสมาชิกของ” เช่น ทุเรียน A, สีแดง B และจะใช้สัญลักษณ์ 
แทนคำว่า “ไม่เป็นสมาชิก ของ” เช่น สีดำ B
ให้ C เป็นเซตของจำนวนเต็มที่น้อยกว่า 3 จะได้ C = {2, 1, 0, -1, …} ในกรณีนี้จะเห็นว่าจำนวนสมาชิกของเซตมีมากมายนับไม่ถ้วน ดังนั้น จึงหา n(C) ไม่ได้ เราเรียกเซตลักษณะนี้ว่า เซตอนันต์ (Infinite Set)
เราสามารถอธิบายเซตในลักษณะเป็นเงื่อนไขแทนการแจกแจงสมาชิก เช่น C={x I | x<3} เมื่อ I เป็นเซตของจำนวนเต็ม
สำหรับเซตที่ไม่มีสมาชิกอยู่เลย จะเรียกว่า เซตว่าง (Empty Set หรือ Null Set) จะใช้สัญลักษณ์ { }, 
เช่น ให้ D เป็นเซตของชื่อจังหวัดในประเทศไทยที่ขึ้นต้นด้วยตัว ฟ จะได้ D={ } และ n(D) = 0
เซตที่มีสมาชิกเหมือนกัน (ตำแหน่งจะสลับกันก็ได้) จะเป็นเซตที่เท่ากันเช่น A = {1, 2, 3} B = {3, 1, 2} กล่าวได้ว่า A = B
โดยปกติแล้ว สมาชิกในเซตจะถูกกำหนดขอบเขตไว้จำกัด จะเรียกขอบเขตนั้นว่าเอกภพสัมพัทธ์ (Universal set) เขียนแทนด้วยสัญลักษณ์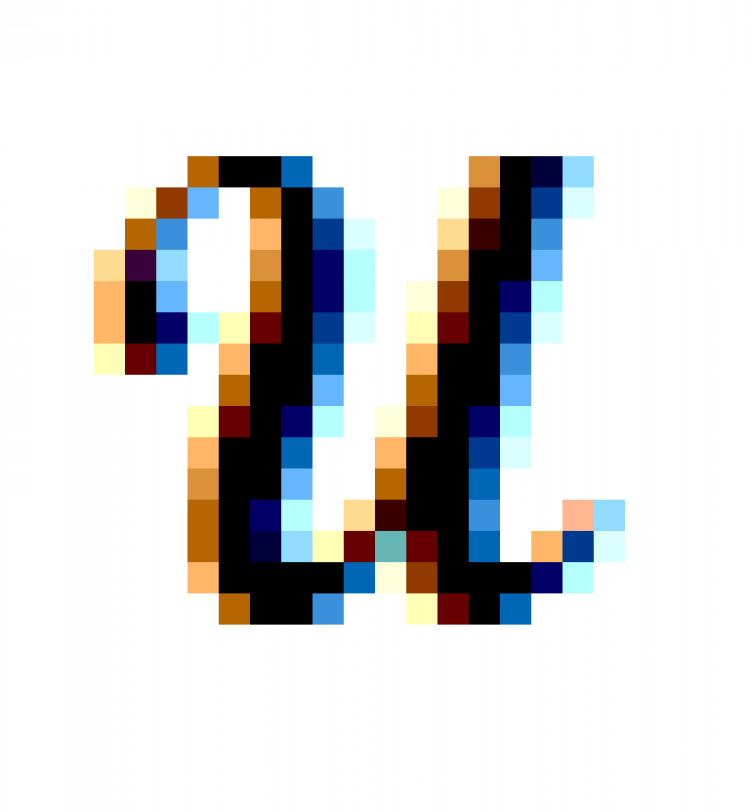 
และสมาชิกของเซตที่กล่าวถึงจะต้องเป็นสมาชิกของ 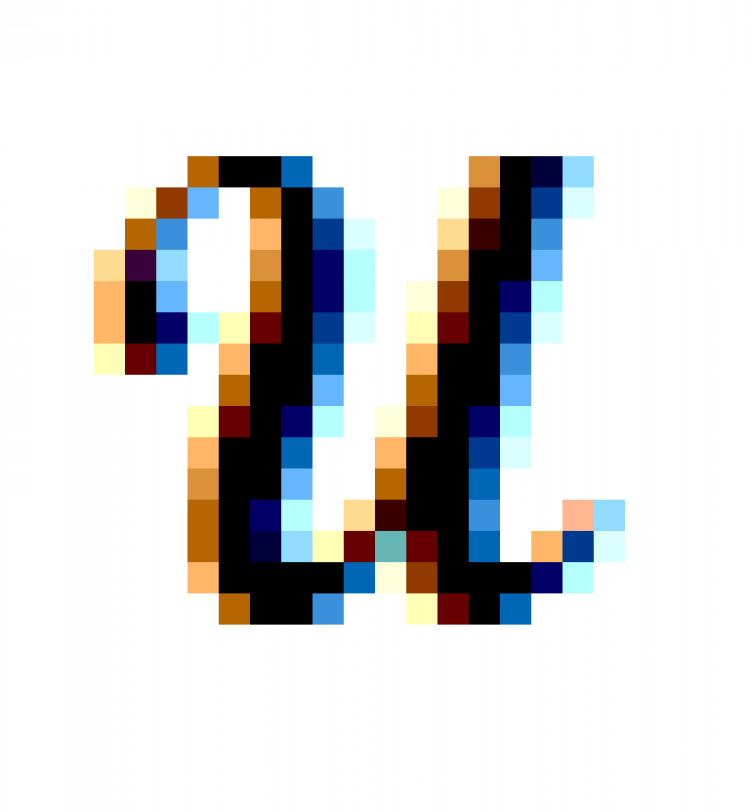เท่านั้น
สับเซต (Subset)
สับเซต หมายถึงเซตย่อย เช่นหากกล่าวว่า B เป็นสับเซตของ A (B
A) ถ้าสมาชิกทุกตัวของ B เป็นสมาชิกของ A
แทนคำว่า “เป็นสมาชิกของ” เช่น ทุเรียน A, สีแดง B และจะใช้สัญลักษณ์ แทนคำว่า “ไม่เป็นสมาชิก ของ” เช่น สีดำ B ให้ C เป็นเซตของจำนวนเต็มที่น้อยกว่า 3 จะได้ C = {2, 1, 0, -1, …} ในกรณีนี้จะเห็นว่าจำนวนสมาชิกของเซตมีมากมายนับไม่ถ้วน ดังนั้น จึงหา n(C) ไม่ได้ เราเรียกเซตลักษณะนี้ว่า เซตอนันต์ (Infinite Set)เราสามารถอธิบายเซตในลักษณะเป็นเงื่อนไขแทนการแจกแจงสมาชิก เช่น C={x
I | x<3} เมื่อ I เป็นเซตของจำนวนเต็ม สำหรับเซตที่ไม่มีสมาชิกอยู่เลย จะเรียกว่า เซตว่าง (Empty Set หรือ Null Set) จะใช้สัญลักษณ์ { }, เช่น ให้ D เป็นเซตของชื่อจังหวัดในประเทศไทยที่ขึ้นต้นด้วยตัว ฟ จะได้ D={ } และ n(D) = 0 เซตที่มีสมาชิกเหมือนกัน (ตำแหน่งจะสลับกันก็ได้) จะเป็นเซตที่เท่ากันเช่น A = {1, 2, 3} B = {3, 1, 2} กล่าวได้ว่า A = B โดยปกติแล้ว สมาชิกในเซตจะถูกกำหนดขอบเขตไว้จำกัด จะเรียกขอบเขตนั้นว่าเอกภพสัมพัทธ์ (Universal set) เขียนแทนด้วยสัญลักษณ์ และสมาชิกของเซตที่กล่าวถึงจะต้องเป็นสมาชิกของ เท่านั้นสับเซต (Subset)
สับเซต หมายถึงเซตย่อย เช่นหากกล่าวว่า B เป็นสับเซตของ A (B
A) ถ้าสมาชิกทุกตัวของ B เป็นสมาชิกของ A
และควรจำไว้ว่า เซตว่างเป็นสับเซตของทุกเซต
Ex จงหาสับเซตทั้งหมดของ A เมื่อ A = {2, 4, 6, 8}
Soln จำนวนสับเซตทั้งหมดหาได้จาก 2n เมื่อ n=จำนวนสมาชิกในเซต
ดังนั้น A จะมีสับเซตทั้งหมด 24=16 สับเซต ดังนี้
{2} {4} {6} {8}
{2, 4} {2, 6} {2, 8} {4, 6} {4, 8} {6, 8}
{2, 4, 6} {2, 6, 8} {2, 4, 8} {4, 6, 8}
{2, 4, 6, 8}
เพาเวอร์เซต (Power set)
หมายถึงเซตของสับเซต จะเขียนแทนเพาเวอร์เซตของเซต A ด้วย P(A)
วิธีหาเพาเวอร์เซต จะต้องหาสับเซตทั้งหมดให้ได้ก่อน จากนั้นจึงใส่เซตครอบลงไป
จากตัวอย่างข้างต้น จะได้เพาเวอร์เซต P(A) = {, {2}, {4}, {6}, {8}, {2, 4}, {2, 6}, {2, 8}, {4, 6}, {4, 8}, {6, 8}, {2, 4, 6}, {2, 6, 8}, {2, 4, 8}, {4, 6, 8}, {2, 4, 6, 8}}
, {2}, {4}, {6}, {8}, {2, 4}, {2, 6}, {2, 8}, {4, 6}, {4, 8}, {6, 8}, {2, 4, 6}, {2, 6, 8}, {2, 4, 8}, {4, 6, 8}, {2, 4, 6, 8}}
ไม่มีความคิดเห็น:
แสดงความคิดเห็น